ipsrdbs1. Introduction to Basic Statistics2. Getting Started with R3. Introduction to Probability4. Conditional Probability and Independence5. Random Variables and Their Probability Distributions6. Standard Discrete Distributions7. Standard Continuous Distributions8. Joint Distributions and the CLT9. Introduction to Statistical Inference10. Methods of Point Estimation11. Interval Estimation12. Hypothesis Testing13. Generating Functions14. Transformation and Transformed Distributions15. Multivariate Distributions16. Convergence of Estimators17. Simple Linear Regression Model18. Multiple Linear Regression Model19. Analysis of VarianceResourcesPdfCorrections
ipsrdbs1. Introduction to Basic Statistics2. Getting Started with R3. Introduction to Probability4. Conditional Probability and Independence5. Random Variables and Their Probability Distributions6. Standard Discrete Distributions7. Standard Continuous Distributions8. Joint Distributions and the CLT9. Introduction to Statistical Inference10. Methods of Point Estimation11. Interval Estimation12. Hypothesis Testing13. Generating Functions14. Transformation and Transformed Distributions15. Multivariate Distributions16. Convergence of Estimators17. Simple Linear Regression Model18. Multiple Linear Regression Model19. Analysis of VarianceResourcesPdfCorrections
16. Convergence of Estimators
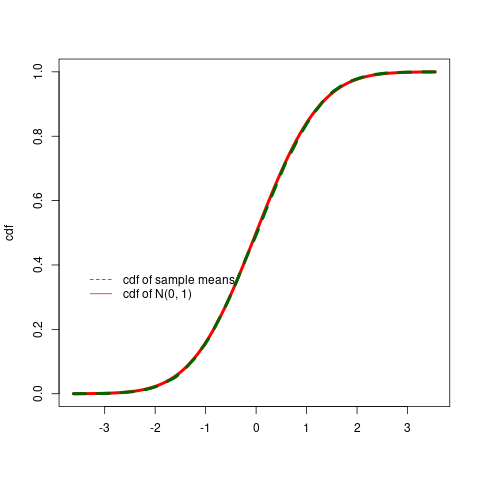
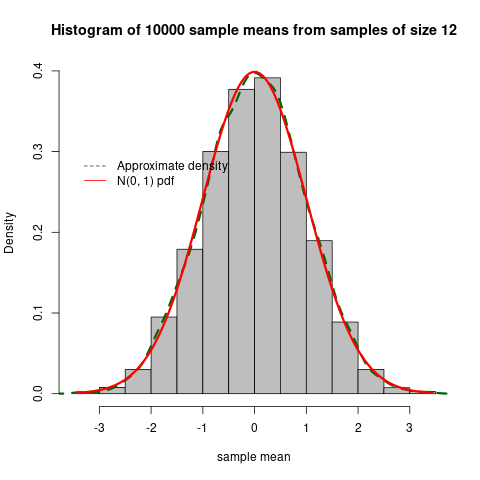
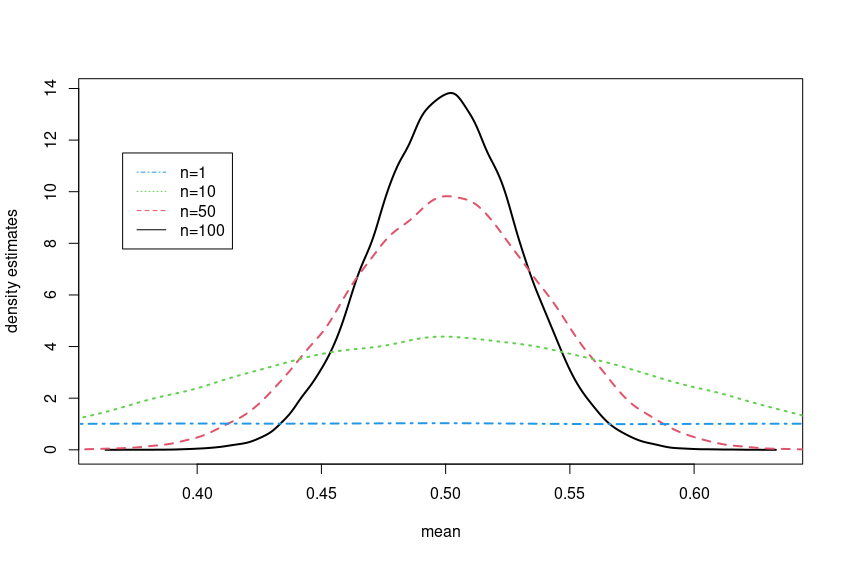
Chapter 16 discusses asymptotic theories which are often required to guarantee good properties of statistical inference techniques. Three types of modes of convergence in statistics are discussed and illustrated with the help of simulation using R routines. Large sample properties of the maximum likelihood estimators are stated and so are the laws of large numbers.
See the Chapter 16 code and output file for the R illustrations provided in this chapter.